PENDULES ET MOUVEMENTS PENDULAIRES

PENDULES ET MOUVEMENTS PENDULAIRES

On appelle pendule un solide pesant soumis à une liaison rotoïde parfaite ou cylindrique ^{[cf. DYNAMIQUE]} par rapport à un repère de référence quelconque (), l’axe du rotoïde ne passant pas par le centre d’inertie G de ce solide (S). Depuis Huygens, la notion de pendule a joué un rôle important dans le développement de la mécanique, d’une part dans la définition des durées égales en chronométrie, d’autre part comme exemple d’application des principes de la dynamique. De plus, on a souvent tendance à dénommer pendule un ensemble de solides animés de mouvements vibratoires assez généraux.

Mouvement pendulaire relatif à un repère galiléen

Étudions d’abord le mouvement d’un seul solide relativement à un repère de référence galiléen (g ) et supposons que l’axe du rotoïde soit O^g z ^g= O^z 轢, faisant avec le plan horizontal du lieu d’expérience un angle 廓 constant (face=F0019 漣 神/2 麗 廓 諒 神/2). Désignons alors par [O| ゑ^s , を^s , ん] un trièdre, lié au solide (S), dont le plan (z Ox ^s ) contient le centre d’inertie G tel que OG= a ゑ^s + c ん, avec a 礪 0 par choix d’orientation de ゑ^s . Si m est la masse de (S) et si l’opérateur d’inertie (I) de (S) en O est représenté dans la base ( ゑ^s , を^s , ん) par la matrice suivante ^{[cf. CINÉTIQUE]}:

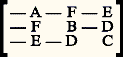Alors les équations du mouvement de (S) sont, dans le cas très général,

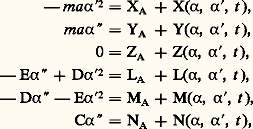où 見 = ( ゑ^g , ゑ^s ) = ( を^g , を^s ) est mesuré sur ん, où (X^A, Y^A, Z^A|L^A, M^A, ^A) sont les composantes sur ( ゑ^s , を^s , ん) des éléments de réduction en O du torseur de liaison exercé par l’articulation rotoïde (N^A = 0 si cette articulation est parfaite) et où (X, Y, Z|L, M, N) sont les composantes sur ( ゑ^s , を^s , ん) des éléments de réduction en O du torseur extérieur connu ^{[cf. DYNAMIQUE]} agissant sur (S); dans le cas de la pesanteur, s = 漣 mg Z^g où Z^g est le vecteur unitaire de la verticale ascendante, 紐⁰ = OG 廬 s ^{[cf. DYNAMIQUE]}, et donc:

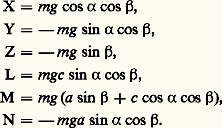Ainsi, les équations du mouvement sont, dans les hypothèses indiquées:

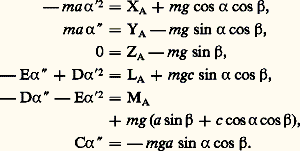Au temps t = 0, 見 et 見 prennent des valeurs 見⁰ et 見 ⁰ que l’on suppose connues; dans ces conditions, la fonction 見(t ) se déduit par intégration de la dernière équation; on calcule ensuite X^A, Y^A, Z^A, L^A, M^A en fonction du temps à l’aide des cinq équations qui précèdent, et le problème est ainsi résolu dans son ensemble.

L’équation différentielle en 見 s’écrit, en posant g ^e = g . cos 廓, où le cas 廓 = 神/2 (c’est-à-dire z ^g vertical) est exclu, et 諸² = mg ^e a /C, où 諸 est la pulsation et C le moment d’inertie de (S) par rapport à Oz 轢:

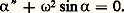On voit que 見 ⁰ = 漣 諸² sin 見⁰ ne peut être nul que si 見⁰ est de sinus nul. Si 見 ⁰ = 0, 見⁰ = 0 correspond à un équilibre stable et 見⁰ = 神 correspond à un équilibre instable. Par intégration, on obtient une équation où les variables se séparent:

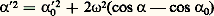ou:

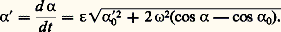Excluant les cas d’équilibre où 見 令 0, on voit que 﨎 = + 1 ou 漣 1 ( 﨎 étant du signe de 見 ⁰ si 見 ⁰ n’est pas nul et du signe de 見⁰ si 見 ⁰ = 0). La fonction t ( 見) est donnée par une intégrale elliptique.

L’expression cos 見 漣 cos 見⁰ + 見 ⁰²/2 諸² doit être positive; si 見 ⁰² 礪 2 諸²(1 + cos 見⁰), cette expression ne s’annule pour aucune valeur de 見, c’est-à-dire que 見 reste du même signe au cours du temps: 見 varie de manière monotone (croissante ou décroissante) et le solide (S) est animé d’un mouvement révolutif qui n’est pas concerné par cette étude; si 見 ⁰² 麗 2 諸²(1 + cos 見⁰), on peut au contraire poser:

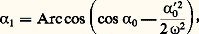et 見 reste compris entre 漣 見¹ et + 見¹; la fonction 見(t ) est alors périodique et de période T telle que:

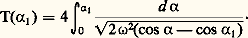On voit que la période des oscillations du pendule (S) dépend de l’amplitude 見¹; on peut, par développement en série, obtenir l’expression suivante de la période:

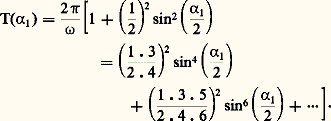Dans le cas où 見¹ est petit, 見 reste petit et l’équation régissant les variations de 見(t ) devient:

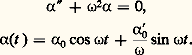Les variations de 見 sont alors sinusoïdales , et la période est:

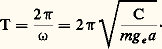Cette formule donne la période à moins de un centième près pour 見¹ 麗 神/8. Si l’on veut avoir une meilleure approximation, il faut prendre les deux premiers termes de l’expression de T( 見¹):

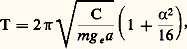et cette formule donne T à moins de un dix-millième près pour 見¹ 麗 神/10. Rappelons que, dans ces relations, C est le moment d’inertie de (S) par rapport à l’axe Ozdu rotoïde:

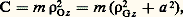où 福^Oz est le rayon de giration de (S) par rapport à Ozet où 福^Gz est le rayon de giration de (S) par rapport à Gz 轢; dans ces conditions, la période des petites oscillations s’écrit:

avec l = a + (1/a) 福^2Gz = l (a ), dite longueur du pendule simple synchrone de (S).

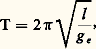On remarque que, pour deux axes Ozet O zsitués de part et d’autre de Gzà des distances a et a liées par aa = 福^2Gz , on a:

c’est-à-dire que (S) oscillera avec la même période si l’axe du rotoïde est Ozou O z(fig. 1).

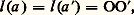La relation de conjugaison entre les axes Ozet O zapparaît encore lorsqu’un pendule subit un choc, c’est-à-dire lorsque 見 (t ) est discontinue et passe brusquement de la valeur 見 ¹ à la valeur 見 ²; les équations régissant le choc sont:

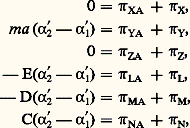où ( 神^XA, 神^YA, 神^ZA| 神^LA, 神^MA, 神^NA) sont les composantes sur ( ゑ^s , を^s , ん) des éléments de réduction en O du torseur de percussion exercé par l’articulation rotoïde au cours du choc ( 神^NA = 0 si l’articulation rotoïde est parfaite); ( 神^X, 神^Y, 神^Z| 神^L, 神^M, 神^N) sont les composantes sur ( ゑ^s , を^s , ん) des éléments de réduction en O du torseur de percussion connu agissant sur (S).

Si l’on cherche les conditions que doit satisfaire le torseur 神 de percussion connu pour que le torseur de percussion exercé par l’articulation soit nul (ce qui signifie que le torseur de liaison a des éléments de réduction qui restent finis au cours du choc), on trouve:

c’est-à-dire que れ 神 = 神^Y . を^s est orthogonal au plan contenant G et l’axe du rotoïde. Dans l’hypothèse où le torseur 神 est un torseur vecteur dont l’axe perce le plan (G, Oz 轢) en I, on a: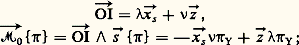

donc: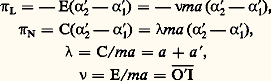

mesuré sur ん.

On dit alors que I est le centre de percussion (fig. 1).

Mouvement pendulaire relatif à un repère quelconque

Comme premier exemple de pendule (S) dont le mouvement est rapporté à un repère quelconque (), considérons le cas où l’axe O size=1^凞z size=1^凞= O^s z ^s= Ozde l’articulation rotoïde ^{[cf. CINÉMATIQUE]} coïncide avec l’axe de révolution d’un cylindre homogène ( 臨) de rayon b et de masse 猪, assujetti à rouler sans glisser sur le plan horizontal (O^g y ^g z ^g ), l’axe ゑ^g étant vertical descendant et les axes を^g et ん étant confondus. Ce cas est celui du pendule d’Euler (fig. 2). Les notations concernant (S) sont les mêmes que précédemment. On note:

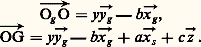K étant le moment d’inertie de ( 臨) par rapport à Oz 轢. On obtient alors la force vive de l’ensemble mécanique constitué de la réunion de (S) et de ( 臨):

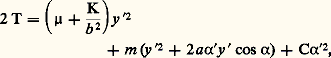ainsi que la puissance galiléenne développée par les efforts agissant sur cet ensemble, le rotoïde d’axe Ozliant (S) et ( 臨) étant supposé parfait,

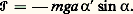Les équations du mouvement de l’ensemble sont alors:

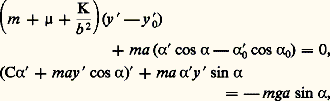ou encore, en reportant la valeur de y déduite de la première des deux équations précédentes,

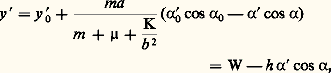avec: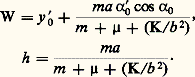

On trouve l’équation différentielle régissant les variations de 見:

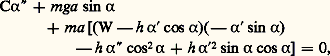qui se réduit à:

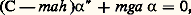dans le cas où 見 et ses dérivées restent petits. On obtient alors:

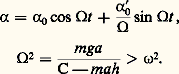Puisque 行 est supérieur à 諸, la période du mouvement 見 a diminué par rapport au cas du pendule précédent.

On remarque qu’au cours du mouvement ainsi créé le cylindre ( 臨) roule avec une vitesse de valeur algébrique moyenne W, c’est-à-dire que, si l’on ne prévoyait pas de butées élastiques pour ( 臨), le système serait animé d’un mouvement pendulaire 見 par rapport au repère () = (O| ゑ^g , を^g , ん), lui-même animé d’un mouvement de translation de vitesse moyenne W を^g .

Pendules entraînés de mouvements donnés

Dans bon nombre d’expériences de mécanique, le solide (S) est animé d’un mouvement tel que le vecteur vitesse ^{(g )}(O^s ) d’un de ses points (à savoir O^s ) est connu à toute date, cependant que l’axe O^s ん^s reste parallèle à une direction ん^g du repère galiléen. Pour de telles études, on pose:

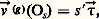où ゝ = ゝ(s ) est un vecteur unitaire tangent en O^s à la trajectoire de O^s , et s l’abscisse curviligne de O^s sur cette trajectoire; la force vive de (S) s’exprime par:

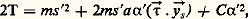cependant que la puissance galiléenne développée par les efforts agissant sur (S) a pour expression:

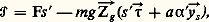où F est la composante sur ゝ de la somme du torseur qui agit extérieurement sur (S) pour communiquer à O^s le mouvement souhaité. Les équations du mouvement sont donc:

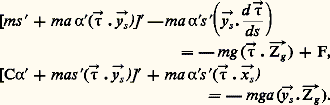La seconde équation permet d’obtenir 見(t ) et la première permet ensuite d’exprimer la fonction requise F pour s (t ) donné.

Il serait possible d’appliquer ces résultats aux cas où:

– le point O^s est animé d’un mouvement rectiligne à accélération constante, c’est-à-dire pour lequel (O^s ) = ⁰(1 + 諸t );

– le point O^s est animé d’un mouvement rectiligne vibratoire simple défini par O^g O^s= a ゎ^g cos 諸t ( ゎ^g vecteur unitaire fixe du galiléen; cas particulier: ゎ^g horizontal ou ゎ^g vertical);

– le point O^s est animé d’un mouvement circulaire uniforme (régulateur de Wright, par exemple).

Pendule multiple

Le problème se complique encore dans le cas du pendule double (et plus généralement du pendule triple et du pendule n -uple) où un solide (S¹) est lié au repère galiléen par une liaison rotoïde parfaite d’axe O^g z ^g= ¹z ¹= Ozet où un solide (S²) est lié au solide (S¹) par une liaison rotoïde parfaite d’axe ²zparallèle au précédent et défini par ¹²= bx ¹(fig. 3).

En utilisant le formalisme lagrangien ^{[cf. MÉCANIQUE ANALYTIQUE]}, on obtient deux équations de mouvement que l’on peut ensuite linéariser ; ce système différentiel s’écrit:

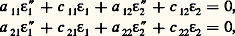où les constantes a ^ij et c ^ij s’expriment à l’aide des caractéristiques géométriques et cinétiques de chacun des solides (S¹) et (S²), cependant que la fonction 﨎^k (t ) définit le mouvement angulaire de S^k à partir de sa position d’équilibre (pour laquelle 見^k prend la valeur 見^{k ,e} ):

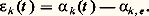Dans le cas particulier du double pendule «ponctuel», on aboutit à un système dont la solution générale est:

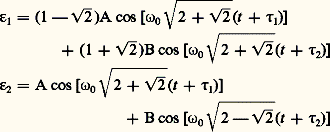Les constantes A, B, 精¹, 精² peuvent s’exprimer en fonction des valeurs prises par 﨎¹, 﨎², 﨎 ¹, 﨎 ² à la date t = 0.

Pendule de Foucault

Dans la célèbre expérience réalisée par Léon Foucault au Panthéon (Paris), le pendule était écarté de sa position initiale et rattaché à un mur par un fil, le pendule étant ainsi immobile par rapport à la Terre. Cette expérience peut actuellement être réalisée au Conservatoire national des arts et métiers (Paris), mais la longueur l du pendule y est très inférieure à 67 m, longueur du pendule original de Foucault. Si on brûle le fil, le pendule se met en mouvement avec une vitesse initiale nulle par rapport à des axes liés à la Terre.

Soit O le point d’attache du pendule, ん^T le vecteur unitaire vertical ascendant (lié à la Terre) au lieu d’expérience (de latitude), ゑ^T le vecteur unitaire dirigé vers le sud et を^T celui qui est dirigé vers l’est; on désignera le repère ainsi défini par (O| ゑ, を, ん) pour simplifier les notations. Les équations du mouvement du pendule sont (en projection sur le plan O ゑを):

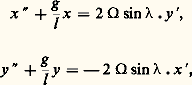où 行 est la vitesse de rotation de la Terre (7,29 憐 10^-5 radian par seconde). On fait intervenir comme variable l’affixe f = x + iy de la projection P (sur x Oy ) du pendule (fig. 4) considéré comme «ponctuel»; l’équation qui régit cet affixe est:

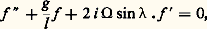et l’on pose:

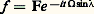ce qui conduit à l’équation différentielle:

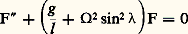régissant l’affixe F de P par rapport aux axes mobiles OXY tels que (face=F0019 轢X, ゑ) = (face=F0019 轢Y, を) = 行t sin (mesuré sur ん). On remarque que 連g/l est de l’ordre de l’unité, tandis que 行 sin est de l’ordre de 10^-5; par conséquent, on peut écrire tout simplement:

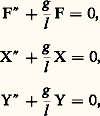L’affixe f étant défini à une constante multiplicative (complexe) près, on peut supposer qu’on ait, à la date t = 0 de début d’expérience,

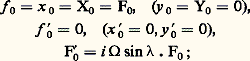donc: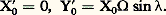

Il en résulte que:

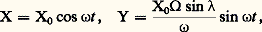avec 諸 = 連g/l .

Ainsi le point P est animé d’un mouvement elliptique par rapport à des axes de référence qui tournent par rapport à la Terre en sens inverse du sens défini sur l’ellipse (trajectoire relative). Dans l’expérience de Foucault, X⁰ = 3 m, la période du mouvement sur l’ellipse est de 16 s, la période de rotation des axes relatifs OXY est 2 神/ 行 sin = 32 h, le rapport des axes de l’ellipse, 諸/ 行 sin est égal à 7 200 (petit axe de l’ordre de 0,8 mm); l’ellipse est tellement aplatie que le mouvement relatif apparaît comme rectiligne et qu’on parle de la rotation du plan z OX (de trajectoire). Ces résultats ont mis en évidence expérimentalement la rotation de la Terre par rapport au repère galiléen.

Encyclopédie Universelle. 2012.